Sprchovacia miestnosť

Horizontálna asymptota a správanie funkcie v nekonečne. Asymptoty funkčných grafov: ich typy, príklady riešení. Vertikálne asymptoty grafu funkcie

Riešenie možno pohodlne rozdeliť do dvoch bodov:

1) Najprv skontrolujeme, či existujú vertikálne asymptoty. Menovateľ ide na nulu a je okamžite jasné, že v tomto bode funkcia trpí nekonečnou diskontinuitou a priamka určená rovnicou je vertikálna asymptota grafu funkcie. Pred vyvodením takéhoto záveru je však potrebné nájsť jednostranné limity:

Pripomínam techniku výpočtu, na ktorú som sa podobne zameral v článku Spojitosť funkcie. Body zlomu. Vo výraze pod limitným znakom dosadíme „X“. V čitateli nie je nič zaujímavé:

Výsledkom menovateľa je však nekonečne malé záporné číslo:

Určuje osud limitu.

Ľavá hranica je nekonečná a v zásade je už možné urobiť úsudok o prítomnosti vertikálnej asymptoty. Ale nielen na to sú potrebné jednostranné limity – POMÁHAJÚ POCHOPIŤ, AKO sa nachádza graf funkcie, a SPRÁVNE ho zostrojiť. Preto musíme vypočítať aj pravotočivý limit:

Záver: jednostranné limity sú nekonečné, čo znamená, že priamka je vertikálna asymptota grafu funkcie at.

Prvý limit je konečný, čo znamená, že musíme „pokračovať v konverzácii“ a nájsť druhý limit:

Druhá hranica je tiež konečná.

Naša asymptota je teda:

Záver: priamka určená rovnicou je horizontálna asymptota grafu funkcie at.

Ak chcete nájsť horizontálnu asymptotu, môžete použiť zjednodušený vzorec:

Ak existuje konečná limita, potom je priamka horizontálnou asymptotou grafu funkcie at.

Je ľahké si všimnúť, že čitateľ a menovateľ funkcie sú rovnakého rádu rastu, čo znamená, že hľadaný limit bude konečný:

Podľa stavu nie je potrebné robiť kresbu, ale ak sme uprostred skúmania funkcie, okamžite urobíme náčrt na návrhu:

Na základe troch zistených limitov skúste sami prísť na to, ako by mohol byť graf funkcie umiestnený. Je to vôbec ťažké? Nájdite 5-6-7-8 bodov a označte ich na výkrese. Graf tejto funkcie je však zostrojený pomocou transformácií grafu elementárnej funkcie a čitatelia, ktorí pozorne skúmali príklad 21 tohto článku, môžu ľahko uhádnuť, o aký druh krivky ide.

Toto je príklad, ktorý môžete vyriešiť sami. Pripomínam, že proces je vhodne rozdelený na dva body – vertikálne asymptoty a šikmé asymptoty. Vo vzorovom riešení sa horizontálna asymptota nájde pomocou zjednodušenej schémy.

V praxi sa najčastejšie stretávame s frakčnými racionálnymi funkciami a po tréningu na hyperbolách si úlohu skomplikujeme:

Nájdite asymptoty grafu funkcie

Riešenie: Raz, dva a hotovo:

1) Vertikálne asymptoty sú v bodoch nekonečnej diskontinuity, takže musíte skontrolovať, či menovateľ ide na nulu. Poďme vyriešiť kvadratickú rovnicu:

Diskriminant je kladný, takže rovnica má dva skutočné korene a práca sa výrazne pridáva

Aby sme ďalej našli jednostranné limity, je vhodné rozložiť štvorcový trinom:

(pre kompaktný zápis bolo „mínus“ zahrnuté v prvej zátvorke). Aby sme boli na bezpečnej strane, skontrolujeme to otvorením zátvoriek v duchu alebo na koncepte.

Prepíšme funkciu vo formulári

Nájdime jednostranné limity v bode:

limit funkcie asymptotného grafu

A v bode:

Priamky sú teda zvislé asymptoty grafu príslušnej funkcie.

2) Ak sa pozriete na funkciu, je celkom zrejmé, že limita bude konečná a máme horizontálnu asymptotu. Ukážme si jeho prítomnosť v krátkosti:

Priamka (os úsečky) je teda horizontálna asymptota grafu tejto funkcie.

Nájdené limity a asymptoty poskytujú veľa informácií o grafe funkcie. Skúste si v duchu predstaviť kresbu s prihliadnutím na nasledujúce skutočnosti:

Načrtnite svoju verziu grafu vo svojom koncepte.

Samozrejme, nájdené limity neurčujú jednoznačne vzhľad grafu a môžete sa pomýliť, ale samotné cvičenie vám poskytne neoceniteľnú pomoc pri kompletnom štúdiu funkcie. Správny obrázok je na konci hodiny.

Nájdite asymptoty grafu funkcie

Sú to úlohy na samostatné riešenie. Obidva grafy majú opäť horizontálne asymptoty, ktoré sú okamžite detegované nasledujúcimi znakmi: v príklade 4 je poradie rastu menovateľa väčšie ako poradie rastu čitateľa a v príklade 5 sú čitateľ a menovateľ rovnaké rovnaké poradie rastu. Vo vzorovom riešení sa prvá funkcia skúma na prítomnosť šikmých asymptot v plnom rozsahu a druhá - cez limit.

Horizontálne asymptoty sú podľa môjho subjektívneho dojmu výrazne bežnejšie ako tie, ktoré sú „skutočne naklonené“. Dlho očakávaný všeobecný prípad:

Nájdite asymptoty grafu funkcie

Riešenie: klasika žánru:

1) Keďže menovateľ je kladný, funkcia je spojitá pozdĺž celej číselnej osi a neexistujú žiadne vertikálne asymptoty. …Je to dobré? Nie je to správne slovo - vynikajúce! Bod č.1 je uzavretý.
2) Skontrolujte prítomnosť šikmých asymptot:

Druhá limita je tiež konečná, preto má graf príslušnej funkcie šikmú asymptotu:

Keď sa teda graf funkcie približuje k priamke nekonečne blízko.

Všimnite si, že v počiatku pretína svoju šikmú asymptotu a takéto priesečníky sú celkom prijateľné - je dôležité, aby „všetko bolo normálne“ v nekonečne (v skutočnosti tu hovoríme o asymptotách).

Nájdite asymptoty grafu funkcie

Riešenie: nie je tu nič zvláštne, čo by som mohol komentovať, preto zostavím približný príklad konečného riešenia:

1) Vertikálne asymptoty. Poďme preskúmať pointu.

Priamka je vertikálna asymptota grafu at.

2) Šikmé asymptoty:

Priamka je šikmá asymptota grafu at.

Nájdené jednostranné limity a asymptoty nám umožňujú s vysokou istotou predpovedať, ako vyzerá graf tejto funkcie.

Nájdite asymptoty grafu funkcie

Toto je príklad nezávislého riešenia, aby ste si uľahčili výpočet niektorých limitov, môžete rozdeliť čitateľa menovateľom podľa členu. Pri analýze výsledkov sa opäť pokúste nakresliť graf tejto funkcie.

Je zrejmé, že vlastníkmi „skutočných“ šikmých asymptot sú grafy tých zlomkových racionálnych funkcií, v ktorých je vedúci stupeň čitateľa o jeden väčší ako vedúci stupeň menovateľa. Ak je to viac, už nebude existovať šikmá asymptota (napríklad).

Ale v živote sa dejú aj iné zázraky.

- (z gréčtiny záporná časť. a symptotos sa zhodujú). Rovná čiara, ktorá sa neustále približuje ku krivke a stretáva sa s ňou až v nekonečne. Slovník cudzích slov zahrnutých v ruskom jazyku. Chudinov A.N., 1910. ASYMPTOTA z... ... Slovník cudzích slov ruského jazyka

ASYMPTOTE- (z gréckeho asymptotos nezhodný), priamka, ku ktorej sa neobmedzene blíži nekonečná vetva krivky, napríklad asymptota hyperboly ... Moderná encyklopédia

ASYMPTOTE- (z gréckeho asymptotos nezhodné) krivka s nekonečnou vetvou, priamka, ku ktorej sa táto vetva neobmedzene približuje, napríklad asymptota hyperboly ... Veľký encyklopedický slovník

asymptota- Priamka s krivkou, ktorá sa k nej postupne približuje. asymptota Priama čiara, ku ktorej krivka nejakej funkcie, ktorá má nekonečnú vetvu, smeruje (bez toho, aby ju niekedy dosiahla), keď jej argument rastie neobmedzene alebo... Technická príručka prekladateľa

Asymptota- (z gréckeho asymptotos nezhodný), priamka, ku ktorej sa neobmedzene približuje nekonečná vetva krivky, napríklad asymptota hyperboly. ... Ilustrovaný encyklopedický slovník

ASYMPTOTE- ženský, geom. priamka, ktorá sa vždy približuje ku krivke (hyperbole), ale nikdy sa s ňou nezbieha. Príklad na vysvetlenie: ak je akékoľvek číslo rozdelené na polovicu, potom sa zníži do nekonečna, ale nikdy sa nestane nulou.... ... Slovník Dahl

asymptota- podstatné meno, počet synoným: 1 riadok (182) ASIS Slovník synonym. V.N. Trishin. 2013… Slovník synonym

Asymptota- (z gréckych slov: a, slnko, piptw) nesúlad. Symptómom sa rozumie čiara, ktorá sa pri neobmedzenom predĺžení približuje k danej zakrivenej čiare alebo jej časti, takže vzdialenosť medzi spoločnými čiarami sa zmenšuje... ...

Asymptota- plocha je priamka pretínajúca plochu aspoň v dvoch bodoch v nekonečne... Encyklopédia Brockhausa a Efrona

ASYMPTOTE- (asymptota) Hodnota, o ktorú sa táto funkcia snaží pri zmene argumentu (argumentu), ale nedosahuje ju pre žiadnu výslednú hodnotu argumentu. Napríklad ak Celkové náklady uvoľnenie x je dané funkciou TC=a+bx, kde a a b sú konštanty... Ekonomický slovník

Asymptota- priamka, ku ktorej smeruje krivka nejakej funkcie (bez toho, aby ju niekedy dosiahla), majúca nekonečnú vetvu, keď jej argument bez obmedzenia rastie alebo klesá. Napríklad vo funkcii: y = c + 1/x sa hodnota y blíži s... ... Ekonomický a matematický slovník

Objavia sa aj problémy, ktoré budete musieť vyriešiť sami, na ktoré môžete vidieť odpovede.

Pojem asymptoty

Ak najskôr zostrojíte asymptoty krivky, potom sa v mnohých prípadoch zjednoduší konštrukcia grafu funkcie.

Osud asymptoty je plný tragédie. Predstavte si, aké to je: celý váš život sa pohybujete v priamej línii k vášmu drahocennému cieľu, približujete sa k nemu čo najbližšie, no nikdy ho nedosiahnete. Napríklad snaha spojiť svoju životnú cestu s cestou požadovanej osoby, v určitom okamihu sa k nej priblížiť takmer blízko, ale ani sa jej nedotknúť. Alebo sa snažte zarobiť miliardu, no pred dosiahnutím tohto cieľa a zápisom do Guinessovej knihy rekordov pre váš prípad chýbajú stotiny centu. Atď. Tak je to aj s asymptotou: neustále sa snaží dosiahnuť krivku grafu funkcie, priblíži sa k nej na minimálnu možnú vzdialenosť, ale nikdy sa jej nedotkne.

Definícia 1. Asymptoty sú tie rovno, ku ktorému sa graf funkcie približuje tak blízko, ako si želáte, keď premenná smeruje k plus nekonečnu alebo mínus nekonečnu.

Definícia 2. Priamka sa nazýva asymptota grafu funkcie, ak vzdialenosť od premenného bodu M graf funkcie až po túto čiaru má tendenciu k nule, keď sa bod nekonečne vzďaľuje M od začiatku pozdĺž ktorejkoľvek vetvy funkčného grafu.

Existujú tri typy asymptot: vertikálne, horizontálne a šikmé.

Vertikálne asymptoty

Prvá vec, ktorú potrebujete vedieť o vertikálnych asymptotách, je, že sú rovnobežné s osou Oj .

Definícia. Rovno X = a je vertikálna asymptota grafu funkcie , ak bod X = a je bod diskontinuity druhého druhu pre túto funkciu.

Z definície vyplýva, že priamka X = a je vertikálna asymptota grafu funkcie f(X) ak je splnená aspoň jedna z podmienok:

V tomto prípade funkcia f(X) nemusí byť vôbec definované, respektíve kedy X ≥ a A X ≤ a .

komentár:

Príklad 1 Graf funkcie r=ln X má vertikálnu asymptotu X= 0 (t. j. zhoduje sa s osou Oj) na hranici definičného oboru, keďže limita funkcie, keďže x smeruje sprava k nule, sa rovná mínus nekonečnu:

(obrázok vyššie).

sami a potom uvidíte riešenia

Príklad 2 Nájdite asymptoty grafu funkcie.

Príklad 3 Nájdite asymptoty grafu funkcie

Horizontálne asymptoty

Prvá vec, ktorú potrebujete vedieť o horizontálnych asymptotách, je, že sú rovnobežné s osou Vôl .

If (limita funkcie ako argument má tendenciu k plus alebo mínus nekonečnu sa rovná určitej hodnote b), To r = b – horizontálna asymptota nepoctivý r = f(X ) (vpravo, keď má X tendenciu k plus nekonečnu, vľavo, keď má X tendenciu k mínus nekonečnu, a obojstranné, ak sú limity, keďže X smeruje k plus alebo mínus nekonečnu, rovnaké).

Príklad 5. Graf funkcie

pri a> 1 opustila horizontálnu asympototu r= 0 (t. j. zhoduje sa s osou Vôl), pretože limit funkcie ako „x“ má tendenciu k mínus nekonečnu je nula:

Krivka nemá pravú horizontálnu asymptotu, pretože limit funkcie ako „x“ má tendenciu k plus nekonečnu sa rovná nekonečnu:

Šikmé asymptoty

Vertikálne a horizontálne asymptoty, ktoré sme skúmali vyššie, sú rovnobežné so súradnicovými osami, takže na ich zostrojenie sme potrebovali len určité číslo – bod na osi x alebo ordináta, ktorým asymptota prechádza. Pre šikmú asymptotu je potrebný väčší sklon k, ktorý ukazuje uhol sklonu čiary a voľný termín b, ktorý ukazuje, koľko je riadok nad alebo pod počiatkom. Tí, ktorí nezabudli na analytickú geometriu az nej na rovnice priamky, si všimnú, že pre šikmú asymptotu nachádzajú rovnica priamky so sklonom. Existenciu šikmej asymptoty určuje nasledujúca veta, na základe ktorej sa nachádzajú práve uvedené koeficienty.

Veta. Ak chcete urobiť krivku r = f(X) mal asymptotu r = kx + b , je potrebné a postačujúce, aby existovali konečné limity k A b uvažovanej funkcie ako má premenná tendenciu X do plus nekonečna a mínus nekonečna:

(1)

(2)

Takto zistené čísla k A b a sú šikmé asymptotné koeficienty.

V prvom prípade (keďže x smeruje k plus nekonečnu) sa získa pravá naklonená asymptota, v druhom prípade (keďže x smeruje k mínus nekonečnu) sa získa ľavá šikmá asymptota. Pravá šikmá asymptota je znázornená na obr. nižšie.

Pri hľadaní rovnice pre šikmú asymptotu je potrebné vziať do úvahy tendenciu X k plus nekonečnu aj mínus nekonečnu. Pre niektoré funkcie, napríklad zlomkové racionálne, sa tieto limity zhodujú, ale pre mnohé funkcie sú tieto limity odlišné a môže existovať iba jedna z nich.

Ak sa limity zhodujú a x má tendenciu k plus nekonečnu a mínus nekonečnu, priamka r = kx + b je obojstranná asymptota krivky.

Ak je aspoň jedna z limít definujúcich asymptotu r = kx + b , neexistuje, potom graf funkcie nemá šikmú asymptotu (ale môže mať zvislú).

Je ľahké vidieť, že horizontálna asymptota r = b je špeciálny prípad šikmého r = kx + b pri k = 0 .

Preto, ak má krivka v akomkoľvek smere horizontálnu asymptotu, potom v tomto smere nie je žiadna naklonená a naopak.

Príklad 6. Nájdite asymptoty grafu funkcie

Riešenie. Funkcia je definovaná na celej číselnej osi okrem X= 0, t.j.

Preto v bode zlomu X= 0 krivka môže mať vertikálnu asymptotu. V skutočnosti, limit funkcie, pretože x má tendenciu k nule zľava, sa rovná plus nekonečnu:

teda X= 0 – vertikálna asymptota grafu tejto funkcie.

Graf tejto funkcie nemá vodorovnú asymptotu, pretože limita funkcie, keďže x smeruje k plus nekonečnu, sa rovná plus nekonečnu:

Zistime prítomnosť šikmej asymptoty:

Má konečné limity k= 2 a b= 0. Rovno r = 2X je obojsmerná šikmá asymptota grafu tejto funkcie (obrázok v príklade).

Príklad 7. Nájdite asymptoty grafu funkcie

Riešenie. Funkcia má jeden bod zlomu X= -1. Vypočítajme jednostranné limity a určme typ diskontinuity:

Záver: X= −1 je bod nespojitosti druhého druhu, teda priamka X= −1 je vertikálna asymptota grafu tejto funkcie.

Hľadáme šikmé asymptoty. Keďže táto funkcia je zlomkovo-racionálna, limity pri a pri sa zhodujú. Nájdeme teda koeficienty na dosadenie priamky - šikmej asymptoty do rovnice:

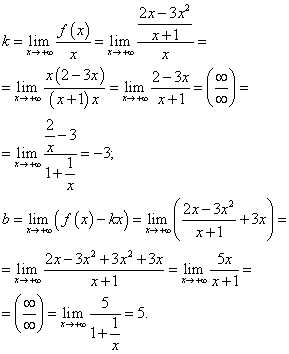
Dosadením nájdených koeficientov do rovnice priamky koeficientom sklonu dostaneme rovnicu šikmej asymptoty:

r = −3X + 5 .

Na obrázku je znázornený graf funkcie bordová farba a asymptoty sú zobrazené čiernou farbou.

Príklad 8. Nájdite asymptoty grafu funkcie

Riešenie. Keďže táto funkcia je spojitá, jej graf nemá žiadne vertikálne asymptoty. Hľadáme šikmé asymptoty:

Graf tejto funkcie má teda asymptotu r= 0 at a nemá asyptot at .

Príklad 9. Nájdite asymptoty grafu funkcie

Riešenie. Najprv hľadáme vertikálne asymptoty. Aby sme to dosiahli, nájdeme doménu definície funkcie. Funkcia je definovaná, keď nerovnosť a . Znak premennej X zodpovedá znameniu. Zvážte preto ekvivalentnú nerovnosť. Z toho dostaneme definičný obor funkcie: . Vertikálna asymptota môže byť len na hranici definičného oboru funkcie. ale X= 0 nemôže byť vertikálna asymptota, pretože funkcia je definovaná v X = 0 .

Zvážte pravostranný limit pri (neexistuje žiadny ľavý limit):

Bodka X= 2 je bod nespojitosti druhého druhu, teda priamka X= 2 - vertikálna asymptota grafu tejto funkcie.

Hľadáme šikmé asymptoty:

takže, r = X+ 1 - šikmá asymptota grafu tejto funkcie pri . Hľadáme šikmú asymptotu na:

takže, r = −X − 1 - šikmá asymptota pri .

Príklad 10. Nájdite asymptoty grafu funkcie

Riešenie. Funkcia má doménu definície . Keďže vertikálna asymptota grafu tejto funkcie môže byť len na hranici definičného oboru, jednostranné limity funkcie nájdeme v .

Asymptoty grafu funkcie

Duch asymptoty sa po stránke potuluje už dlho, aby sa nakoniec zhmotnil v samostatnom článku a priniesol mimoriadnu radosť čitateľom, ktorí sú zmätení úplné štúdium funkcie. Hľadanie asymptot grafu je jednou z mála častí tejto úlohy, ktorá je v školskom kurze pokrytá len prehľadne, keďže udalosti sa točia okolo výpočtu limity funkcií, ale stále súvisia vyššia matematika. Pre návštevníkov, ktorí málo rozumejú matematickej analýze, myslím, že nápoveda je jasná ;-) ...prestaň, prestaň, kam ideš? Limity- je to ľahké!

Príklady asymptot sme narazili hneď v prvej lekcii o grafy elementárnych funkcií a téma sa teraz podrobne posudzuje.

Čo je teda asymptota?

Predstavte si variabilný bod, ktorý „cestuje“ po grafe funkcie. Asymptota je rovno, ku ktorému na neurčito zavrieť graf funkcie sa približuje, keď sa jej premenný bod pohybuje do nekonečna.

Poznámka : Definícia má zmysel, ak potrebujete formuláciu v matematickej notácii, pozrite si učebnicu.

V rovine sú asymptoty klasifikované podľa ich prirodzeného umiestnenia:

1) Vertikálne asymptoty, ktoré sú dané rovnicou v tvare , kde „alfa“ je reálne číslo. Populárny predstaviteľ definuje samotnú ordinátovú os,
s miernym pocitom nevoľnosti si spomíname na hyperbolu.

2) Šikmé asymptoty tradične napísané rovnica priamky s uhlovým koeficientom. Niekedy samostatná skupina zvýrazniť špeciálny prípad - horizontálne asymptoty. Napríklad rovnaká hyperbola s asymptotou.

Poďme rýchlo, zasiahneme tému krátkym výbuchom guľometnej paľby:

Koľko asymptot môže mať graf funkcie?

Nie jeden, jeden, dva, tri,... alebo nekonečne veľa. Po príklady nepôjdeme ďaleko, zapamätajme si elementárne funkcie. Parabola, kubická parabola a sínusová vlna nemajú vôbec asymptoty. exponenciálny graf, logaritmická funkcia má jedinečnú asymptotu. Arkustangens a arkotangens ich majú dve a tangens a kotangens ich má nekonečne veľa. Nie je nezvyčajné, že graf má horizontálne aj vertikálne asymptoty. Hyperbola, vždy ťa bude milovať.

Čo znamená ?

Vertikálne asymptoty grafu funkcie

Zvyčajne sa nachádza vertikálna asymptota grafu v bode nekonečnej diskontinuity funkcie. Je to jednoduché: ak má funkcia v určitom bode nekonečnú diskontinuitu, potom je priamka určená rovnicou vertikálnou asymptotou grafu.

Poznámka : Všimnite si, že záznam sa používa na označenie dvoch úplne odlišných konceptov. Či ide o bod alebo rovnicu priamky, závisí od kontextu.

Na zistenie prítomnosti vertikálnej asymptoty v bode to stačí ukázať aspoň jeden z jednostranných limitov nekonečné. Najčastejšie je to bod, kde je menovateľ funkcie nula. Vertikálne asymptoty sme v podstate už našli v posledných príkladoch lekcie o kontinuite funkcie. Ale v niektorých prípadoch existuje len jedna jednostranná hranica, a ak je nekonečná, potom znova - milujte a uprednostňujte vertikálnu asymptotu. Najjednoduchšia ilustrácia: a ordináta osi (pozri. Grafy a vlastnosti elementárnych funkcií).

Z vyššie uvedeného tiež vyplýva jednoznačný fakt: ak je funkcia nepretržite zapnutá, potom neexistujú žiadne vertikálne asymptoty. Z nejakého dôvodu mi napadla parabola. Ozaj, kde tu môžete „prilepiť“ rovnú čiaru? ...áno...rozumiem... Priaznivci strýka Freuda začali byť hysterické =)

Opačné tvrdenie je vo všeobecnosti nepravdivé: napríklad funkcia nie je definovaná na celej číselnej osi, ale je úplne zbavená asymptot.

Šikmé asymptoty grafu funkcie

Šikmé (ako špeciálny prípad - horizontálne) asymptoty možno nakresliť, ak argument funkcie smeruje k „plus nekonečnu“ alebo k „mínus nekonečnu“. Preto graf funkcie nemôže mať viac ako dve šikmé asymptoty. Napríklad graf exponenciálnej funkcie má jednu horizontálnu asymptotu v , a graf arkustangensu v má dve takéto asymptoty a rôzne.

Keď sa graf na oboch miestach približuje k jedinej šikmej asymptote, potom sa „nekonečná“ zvyčajne kombinujú pod jeden záznam. Napríklad ...uhádli ste správne: .

Všeobecné pravidlo:

Ak sú dve Konečný limit , potom je priamka šikmá asymptota grafu funkcie v . Ak aspoň jeden z uvedených limitov je nekonečno, potom neexistuje žiadna šikmá asymptota.

Poznámka : vzorce zostávajú platné, ak „x“ smeruje iba k „plus nekonečnu“ alebo iba k „mínus nekonečnu“.

Ukážme, že parabola nemá žiadne šikmé asymptoty:

Limita je nekonečná, čo znamená, že neexistuje žiadna šikmá asymptota. Všimnite si, že pri hľadaní limitu potreba zmizla, keďže odpoveď už bola prijatá.

Poznámka : Ak máte (alebo budete mať) ťažkosti s porozumením znamienkam plus-mínus, mínus-plus, pozrite si pomoc na začiatku lekcie
na infinitezimálnych funkciách, kde som vám povedal, ako správne interpretovať tieto znaky.

Je zrejmé, že akákoľvek kvadratická, kubická funkcia, polynóm 4. a vyššieho stupňa tiež nemá šikmé asymptoty.

Teraz sa presvedčíme, že graf tiež nemá šikmú asymptotu. Na odhalenie neistoty používame L'Hopitalovo pravidlo:
, čo bolo potrebné skontrolovať.

Keď funkcia rastie donekonečna, no neexistuje priamka, ku ktorej by sa jej graf približoval nekonečne blízko.

Prejdime k praktickej časti lekcie:

Ako nájsť asymptoty grafu funkcie?

Presne tak je formulovaná typická úloha a zahŕňa nájdenie VŠETKÝCH asymptot grafu (vertikálne, naklonené/horizontálne). Aj keď, aby sme boli presnejší pri položení otázky, hovoríme o výskume prítomnosti asymptot (napokon nemusia byť žiadne). Začnime niečím jednoduchým:

Príklad 1

Nájdite asymptoty grafu funkcie

Riešenie Je vhodné rozdeliť ho do dvoch bodov:

1) Najprv skontrolujeme, či existujú vertikálne asymptoty. Menovateľ ide na nulu a hneď je jasné, že v tomto bode funkcia trpí nekonečná medzera a priamka daná rovnicou je vertikálna asymptota grafu funkcie. Pred vyvodením takéhoto záveru je však potrebné nájsť jednostranné limity:

Pripomínam techniku výpočtu, na ktorú som sa podobne zameral v článku Kontinuita funkcie. Body zlomu. Vo výraze pod limitným znakom dosadíme . V čitateli nie je nič zaujímavé:
.

Ale v menovateli to dopadá nekonečne malé záporné číslo:
, určuje osud limitu.

Ľavá hranica je nekonečná a v zásade je už možné urobiť úsudok o prítomnosti vertikálnej asymptoty. Ale nielen na to sú potrebné jednostranné limity – POMÁHAJÚ ROZUMIEŤ AKO nájdite graf funkcie a vytvorte ho SPRÁVNE. Preto musíme vypočítať aj pravotočivý limit:

Záver: jednostranné limity sú nekonečné, čo znamená, že priamka je vertikálna asymptota grafu funkcie v .

Prvý limit konečný, čo znamená, že je potrebné „pokračovať v konverzácii“ a nájsť druhý limit:

Aj druhý limit konečný.

Naša asymptota je teda:

Záver: priamka daná rovnicou je horizontálna asymptota grafu funkcie v .

Na nájdenie horizontálnej asymptoty
môžete použiť zjednodušený vzorec:

Ak existuje konečný limita, potom je priamka horizontálnou asymptotou grafu funkcie v .

Je ľahké vidieť, že čitateľ a menovateľ funkcie rovnaké poradie rastu, čo znamená, že hľadaná limita bude konečná:

Odpoveď:

Podľa stavu nemusíte kresliť, ale ak je v plnom prúde funkčná štúdia, potom na návrhu okamžite urobíme náčrt:

Na základe troch nájdených limitov skúste sami prísť na to, ako by mohol byť umiestnený graf funkcie. Je to vôbec ťažké? Nájdite 5-6-7-8 bodov a označte ich na výkrese. Graf tejto funkcie je však skonštruovaný pomocou transformácie grafu elementárnej funkcie a čitatelia, ktorí pozorne preskúmali príklad 21 vyššie uvedeného článku, môžu ľahko uhádnuť, o aký druh krivky ide.

Príklad 2

Nájdite asymptoty grafu funkcie

Toto je príklad, ktorý môžete vyriešiť sami. Pripomínam, že je vhodné rozdeliť proces na dva body – vertikálne asymptoty a šikmé asymptoty. Vo vzorovom riešení sa horizontálna asymptota nájde pomocou zjednodušenej schémy.

V praxi sa najčastejšie stretávame s frakčnými racionálnymi funkciami a po tréningu na hyperbolách si úlohu skomplikujeme:

Príklad 3

Nájdite asymptoty grafu funkcie

Riešenie: Raz, dva a hotovo:

1) Sú umiestnené vertikálne asymptoty v bodoch nekonečnej diskontinuity, takže musíte skontrolovať, či je menovateľ nulový. Rozhodnime sa kvadratická rovnica:

Diskriminant je kladný, takže rovnica má dva skutočné korene a práca sa výrazne zvyšuje =)

Aby bolo možné ďalej nájsť jednostranné limity, je vhodné faktorizovať štvorcovú trojčlenku:
(pre kompaktný zápis bolo „mínus“ zahrnuté v prvej zátvorke). Aby sme boli na bezpečnej strane, skontrolujeme to otvorením zátvoriek v duchu alebo na koncepte.

Prepíšme funkciu vo formulári

Nájdime jednostranné limity v bode:

A v bode:

Priamky sú teda zvislé asymptoty grafu príslušnej funkcie.

2) Ak sa pozriete na funkciu , potom je celkom zrejmé, že limita bude konečná a máme horizontálnu asymptotu. Ukážme si jeho prítomnosť v krátkosti:

Priamka (os úsečky) je teda horizontálna asymptota grafu tejto funkcie.

Odpoveď:

Nájdené limity a asymptoty poskytujú veľa informácií o grafe funkcie. Skúste si v duchu predstaviť kresbu s prihliadnutím na nasledujúce skutočnosti:

Načrtnite svoju verziu grafu vo svojom koncepte.

Samozrejme, nájdené limity neurčujú jednoznačne vzhľad grafu a môžete sa pomýliť, ale samotné cvičenie vám poskytne neoceniteľnú pomoc pri plne funkčné štúdium. Správny obrázok je na konci hodiny.

Príklad 4

Nájdite asymptoty grafu funkcie

Príklad 5

Nájdite asymptoty grafu funkcie

Sú to úlohy na samostatné riešenie. Oba grafy majú opäť vodorovné asymptoty, ktoré sú okamžite zistené nasledujúcimi vlastnosťami: v príklade 4 poradie rastu menovateľ viac, ako je poradie rastu čitateľa a v príklade 5 čitateľa a menovateľa rovnaké poradie rastu. Vo vzorovom riešení sa prvá funkcia skúma na prítomnosť šikmých asymptot v plnom rozsahu a druhá cez limit.

Horizontálne asymptoty sú podľa môjho subjektívneho dojmu výrazne bežnejšie ako tie, ktoré sú „skutočne naklonené“. Dlho očakávaný všeobecný prípad:

Príklad 6

Nájdite asymptoty grafu funkcie

Riešenie: klasika žánru:

1) Keďže menovateľ je kladný, potom funkcia nepretržitý pozdĺž celej číselnej osi a neexistujú žiadne vertikálne asymptoty. …Je to dobré? Nie je to správne slovo - vynikajúce! Bod č.1 je uzavretý.

2) Skontrolujte prítomnosť šikmých asymptot:

Prvý limit konečný, tak poďme ďalej. Počas výpočtu druhého limitu eliminovať neistota "nekonečno mínus nekonečno" Prinášame výraz k spoločnému menovateľovi: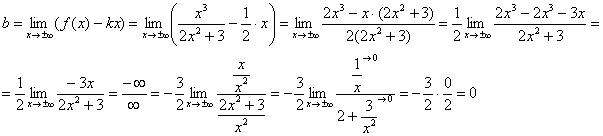

Aj druhý limit konečný Preto má graf príslušnej funkcie šikmú asymptotu:

Záver:

Keď teda graf funkcie nekonečne blízko blíži sa k priamke:

Príklad 7

Nájdite asymptoty grafu funkcie

Riešenie: Nie je tu nič zvláštne, čo by som mohol komentovať, preto nakreslím približný príklad čistého riešenia:

1) Vertikálne asymptoty. Poďme preskúmať pointu.

Priamka je vertikálna asymptota grafu v .

2) Šikmé asymptoty:

Priamka je šikmá asymptota grafu v .

Odpoveď:

Nájdené jednostranné limity a asymptoty nám umožňujú s vysokou istotou predpovedať, ako vyzerá graf tejto funkcie. Správna kresba na konci hodiny.

Príklad 8

Nájdite asymptoty grafu funkcie

Je zrejmé, že vlastníkmi „skutočných“ šikmých asymptot sú grafy tých zlomkových racionálnych funkcií, ktorých najvyšší stupeň čitateľa ešte jeden najvyšší stupeň menovateľa. Ak je to viac, nebude existovať žiadna šikmá asymptota (napríklad ).

Ale v živote sa dejú aj iné zázraky:

Príklad 9

Príklad 11

Preskúmajte graf funkcie na prítomnosť asymptot

Riešenie: to je jasné , preto uvažujeme len pravú polrovinu, kde je graf funkcie.

Priamka (ordináta osi) je teda vertikálna asymptota pre graf funkcie v .

2) Štúdia na šikmej asymptote môže byť vykonaná podľa úplnej schémy, ale v článku L'Hopitalove pravidlá zistili sme to lineárna funkcia viac vysoký poriadok rast ako logaritmický, preto: (Pozri príklad 1 tej istej lekcie).