Sala de dus

Asimptotă orizontală și comportamentul unei funcții la infinit. Asimptote ale graficelor de funcții: tipurile lor, exemple de soluții. Asimptotele verticale ale graficului unei funcții

Soluția poate fi împărțită convenabil în două puncte:

1) Mai întâi verificăm dacă există asimptote verticale. Numitorul ajunge la zero la, și este imediat clar că în acest punct funcția suferă o discontinuitate infinită, iar linia dreaptă specificată de ecuație este asimptota verticală a graficului funcției. Dar, înainte de a trage o astfel de concluzie, este necesar să se găsească limite unilaterale:

Vă reamintesc de tehnica de calcul pe care m-am concentrat în mod similar în articolul Continuitatea unei funcții. Puncte de rupere. Înlocuim „X” în expresia de sub semnul limită. Nu există nimic interesant în numărător:

Dar numitorul are ca rezultat un număr negativ infinitezimal:

Ea determină soarta limitei.

Limita din stânga este infinită și, în principiu, este deja posibil să se pronunțe despre prezența unei asimptote verticale. Dar limitele unilaterale sunt necesare nu numai pentru aceasta, ci AJUTĂ LA ÎNȚELEGEREA CUM este situat graficul unei funcții și la construirea CORECT. Prin urmare, trebuie să calculăm și limita pentru dreapta:

Concluzie: limitele unilaterale sunt infinite, ceea ce înseamnă că linia dreaptă este asimptota verticală a graficului funcției la.

Prima limită este finită, ceea ce înseamnă că trebuie să „continuăm conversația” și să găsim a doua limită:

A doua limită este, de asemenea, finită.

Astfel, asimptota noastră este:

Concluzie: linia dreaptă specificată de ecuație este asimptota orizontală a graficului funcției at.

Pentru a găsi asimptota orizontală, puteți utiliza o formulă simplificată:

Dacă există o limită finită, atunci linia dreaptă este asimptota orizontală a graficului funcției la.

Este ușor de observat că numărătorul și numitorul funcției sunt de aceeași ordine de creștere, ceea ce înseamnă că limita căutată va fi finită:

În funcție de condiție, nu este nevoie să facem un desen, dar dacă ne aflăm în mijlocul cercetării unei funcții, atunci facem imediat o schiță asupra schiței:

Pe baza celor trei limite găsite, încercați să vă dați seama singur cum ar putea fi localizat graficul funcției. Este deloc greu? Găsiți 5-6-7-8 puncte și marcați-le pe desen. Cu toate acestea, graficul acestei funcții este construit folosind transformări ale graficului unei funcții elementare, iar cititorii care au examinat cu atenție Exemplul 21 din articolul de mai sus pot ghici cu ușurință ce fel de curbă este aceasta.

Acesta este un exemplu de rezolvat singur. Permiteți-mi să vă reamintesc că procesul este împărțit convenabil în două puncte - asimptote verticale și asimptote oblice. În soluția eșantion, asimptota orizontală este găsită folosind o schemă simplificată.

În practică, funcțiile fracționale-raționale sunt cel mai des întâlnite, iar după antrenamentul pe hiperbole, vom complica sarcina:

Găsiți asimptotele graficului unei funcții

Soluție: unu, doi și gata:

1) Asimptotele verticale sunt în puncte de discontinuitate infinită, așa că trebuie să verificați dacă numitorul ajunge la zero. Să rezolvăm ecuația pătratică:

Discriminantul este pozitiv, deci ecuația are două rădăcini reale, iar munca se adaugă semnificativ

Pentru a găsi în continuare limite unilaterale, este convenabil să factorizezi trinomul pătrat:

(pentru notarea compactă, „minus” a fost inclus în prima paranteză). Pentru a fi în siguranță, haideți să verificăm prin deschiderea parantezelor mental sau la curent.

Să rescriem funcția în formă

Să găsim limite unilaterale la punctul:

limita funcției graficului asimptot

Și la punctul:

Astfel, liniile drepte sunt asimptote verticale ale graficului funcției în cauză.

2) Dacă te uiți la funcție, este destul de evident că limita va fi finită și avem o asimptotă orizontală. Să-i arătăm prezența pe scurt:

Astfel, linia dreaptă (axa absciselor) este asimptota orizontală a graficului acestei funcții.

Limitele și asimptotele găsite oferă o mulțime de informații despre graficul funcției. Încercați să vă imaginați mental desenul ținând cont de următoarele fapte:

Schițați versiunea dvs. a graficului pe schița dvs.

Desigur, limitele găsite nu determină în mod clar aspectul graficului și este posibil să faceți o greșeală, dar exercițiul în sine va oferi o asistență neprețuită în cursul unui studiu complet al funcției. Poza corectă este la sfârșitul lecției.

Găsiți asimptotele graficului unei funcții

Acestea sunt sarcini pentru soluții independente. Ambele grafice au din nou asimptote orizontale, care sunt detectate imediat de următoarele caracteristici: în exemplul 4, ordinea de creștere a numitorului este mai mare decât ordinea de creștere a numărătorului, iar în exemplul 5, numărătorul și numitorul sunt de aceeași ordine de creștere. În soluția de probă, prima funcție este examinată pentru prezența asimptotelor oblice în întregime, iar a doua - prin limită.

Asimptotele orizontale, în impresia mea subiectivă, sunt vizibil mai frecvente decât cele care sunt „cu adevărat înclinate”. Cazul general mult așteptat:

Găsiți asimptotele graficului unei funcții

Soluție: clasic al genului:

1) Deoarece numitorul este pozitiv, funcția este continuă de-a lungul întregii drepte numerice și nu există asimptote verticale. ...Este bun? Nu este cuvântul potrivit - excelent! Punctul nr. 1 este închis.
2) Să verificăm prezența asimptotelor oblice:

A doua limită este, de asemenea, finită, prin urmare, graficul funcției în cauză are o asimptotă oblică:

Astfel, atunci când graficul funcției se apropie de o dreaptă infinit apropiată.

Rețineți că își intersectează asimptota oblică la origine și astfel de puncte de intersecție sunt destul de acceptabile - este important ca „totul este normal” la infinit (de fapt, aici vorbim despre asimptote).

Găsiți asimptotele graficului unei funcții

Soluție: nu este nimic special de comentat, așa că voi întocmi un exemplu aproximativ de soluție finală:

1) Asimptote verticale. Să explorăm ideea.

Linia dreaptă este asimptota verticală pentru graficul la.

2) Asimptote oblice:

Linia dreaptă este asimptota înclinată pentru graficul la.

Limitele și asimptotele unilaterale găsite ne permit să prezicem cu mare încredere cum arată graficul acestei funcții.

Găsiți asimptotele graficului unei funcții

Acesta este un exemplu de soluție independentă, pentru comoditatea calculării unor limite, puteți împărți numeratorul la numitor termen cu termen. Din nou, atunci când analizați rezultatele, încercați să desenați un grafic al acestei funcții.

Evident, deținătorii de asimptote oblice „reale” sunt graficele acelor funcții raționale fracționale în care gradul cel mai înalt al numărătorului este cu unul mai mare decât gradul cel mai înalt al numitorului. Dacă este mai mult, nu va mai exista o asimptotă oblică (de exemplu).

Dar alte miracole se întâmplă în viață.

- (din greacă o parte negativă., iar symptotos coincid împreună). O linie dreaptă care se apropie constant de o curbă și o întâlnește doar la infinit. Dicționar de cuvinte străine incluse în limba rusă. Chudinov A.N., 1910. ASIMPTOTA din... ... Dicționar de cuvinte străine ale limbii ruse

ASIMPTOTĂ- (din grecescul asymptotos necoincident), o linie dreaptă de care se apropie fără limită o ramură infinită a unei curbe, de exemplu asimptota unei hiperbole... Enciclopedie modernă

ASIMPTOTĂ- (din grecescul asymptotos necoincident) o curbă cu o ramură infinită, o linie dreaptă de care această ramură se apropie fără limită, de exemplu, asimptota unei hiperbole... Dicţionar enciclopedic mare

asimptotă- O linie dreaptă cu o curbă care se apropie treptat de ea. asimptotă Linie dreaptă spre care curba unei funcții, având o ramură infinită, tinde (fără să ajungă vreodată la ea) atunci când argumentul său crește fără limită sau...

Ghidul tehnic al traducătorului- (din grecescul asymptotos necoincident), linie dreaptă de care se apropie fără limită o ramură infinită a unei curbe, de exemplu asimptota unei hiperbole. ... Dicţionar Enciclopedic Ilustrat

ASIMPTOTĂ- femeie, geom. o linie dreaptă, care se apropie mereu de o curbă (hiperbolă), dar nu converge niciodată cu aceasta. Un exemplu pentru a explica acest lucru: dacă orice număr este împărțit la jumătate, atunci va scădea la infinit, dar nu va deveni niciodată zero.... ... Dicţionar Dahl

asimptotă- substantiv, număr de sinonime: 1 rând (182) Dicţionar de Sinonime ASIS. V.N. Trishin. 2013… Dicţionar de sinonime

Ghidul tehnic al traducătorului- (din cuvintele grecești: a, sun, piptw) nepotriviți. Prin simptom se înțelege o linie care, fiind extinsă la infinit, se apropie de o anumită linie curbă sau de o parte a acesteia, astfel încât distanța dintre liniile comune devine mai mică... ...

Ghidul tehnic al traducătorului- o suprafață este o linie dreaptă care intersectează suprafața în cel puțin două puncte la infinit... Enciclopedia lui Brockhaus și Efron

ASIMPTOTĂ- (asimptotă) Valoarea la care se străduiește această funcție atunci când schimbă argumentul (argumentul), dar nu o atinge pentru nicio valoare finală a argumentului. De exemplu, dacă cost total eliberarea x este dată de funcția TC=a+bx, unde a și b sunt constante... Dicționar economic

Ghidul tehnic al traducătorului- o linie dreaptă spre care tinde curba unei funcții (fără a ajunge vreodată la ea), având o ramură infinită, când argumentul său crește sau scade fără limită. De exemplu, în funcția: y = c + 1/x valoarea lui y se apropie cu... ... Dicționar economic și matematic

Vor fi, de asemenea, probleme pe care le rezolvați singur, la care puteți vedea răspunsurile.

Conceptul de asimptotă

Dacă construiți mai întâi asimptotele curbei, atunci în multe cazuri construcția unui grafic al funcției devine mai ușoară.

Soarta asimptotei este plină de tragedie. Imaginează-ți cum este: toată viața ta mergând în linie dreaptă către obiectivul tău prețuit, apropiindu-te cât mai mult posibil de el, dar fără a-l atinge niciodată. De exemplu, străduindu-te să-ți conectezi drumul vieții cu drumul persoanei dorite, la un moment dat apropiindu-te de el aproape îndeaproape, dar nici măcar nu atingându-l. Sau străduiește-te să câștigi un miliard, dar înainte de a atinge acest obiectiv și de a intra în Cartea Recordurilor Guinness pentru cazul tău, lipsesc sutimi de cent. Și altele asemenea. Așa este și cu o asimptotă: se străduiește constant să ajungă la curba graficului funcției, se apropie de ea la distanța minimă posibilă, dar nu o atinge niciodată.

Definiție 1. Asimptotele sunt acelea Drept, de care graficul unei funcții se apropie cât se dorește atunci când variabila tinde spre plus infinit sau minus infinit.

Definiția 2. O linie dreaptă se numește asimptotă a graficului unei funcții dacă distanța de la punctul variabil M graficul funcției până la această dreaptă tinde spre zero pe măsură ce punctul se îndepărtează la infinit M de la origine de-a lungul oricărei ramuri a graficului funcției.

Există trei tipuri de asimptote: verticale, orizontale și oblice.

Asimptote verticale

Primul lucru pe care trebuie să-l știți despre asimptotele verticale este că sunt paralele cu axa Oi .

Definiţie. Drept x = o este asimptotă verticală a graficului funcției , dacă punct x = o este punct de discontinuitate de al doilea fel pentru această funcție.

Din definiție rezultă că linia dreaptă x = o este asimptota verticală a graficului funcției f(x) dacă este îndeplinită cel puțin una dintre condiții:

În acest caz, funcția f(x) poate să nu fie definită deloc, respectiv, când x ≥ oŞi x ≤ o .

Comentariu:

Exemplul 1. Graficul unei funcții y=ln x are o asimptotă verticală x= 0 (adică coincide cu axa Oi) la limita domeniului de definitie, deoarece limita functiei ca x tinde spre zero de la dreapta este egala cu minus infinit:

(poza de mai sus).

tu și apoi vezi soluțiile

Exemplul 2. Găsiți asimptotele graficului funcției.

Exemplul 3. Găsiți asimptotele graficului unei funcții

Asimptote orizontale

Primul lucru pe care trebuie să-l știți despre asimptotele orizontale este că sunt paralele cu axa Bou .

Dacă (limita unei funcție, deoarece argumentul tinde spre plus sau minus infinit este egală cu o anumită valoare b), Asta y = b – asimptotă orizontală strâmb y = f(x ) (dreapta când X tinde spre plus infinit, stânga când X tinde spre minus infinit și cu două fețe dacă limitele ca X tinde spre plus sau minus infinit sunt egale).

Exemplul 5. Graficul unei funcții

la o> 1 a lăsat asimpot orizontal y= 0 (adică coincide cu axa Bou), deoarece limita funcției ca „x” tinde spre minus infinit este zero:

Curba nu are o asimptotă orizontală dreaptă, deoarece limita funcției ca „x” tinde spre plus infinit este egală cu infinit:

Asimptote oblice

Asimptotele verticale și orizontale pe care le-am examinat mai sus sunt paralele cu axele de coordonate, așa că pentru a le construi am avut nevoie doar de un anumit număr - punctul de pe axa abscisă sau ordonată prin care trece asimptota. Pentru o asimptotă oblică, este necesară o pantă mai mare k, care arată unghiul de înclinare al dreptei, și termenul liber b, care arată cât de mult este linia deasupra sau sub origine. Cei care nu au uitat geometria analitică, și din ea ecuațiile dreptei, vor observa că pentru asimptota oblică găsesc ecuația unei drepte cu panta. Existența unei asimptote oblice este determinată de următoarea teoremă, pe baza căreia se găsesc coeficienții tocmai menționați.

Teorema. Pentru a face curba y = f(x) avea o asimptotă y = kx + b , este necesar și suficient ca să existe limite finite kŞi b a funcţiei luate în considerare pe măsură ce variabila tinde x la plus infinit și minus infinit:

(1)

(2)

Cifrele găsite în acest fel kŞi bși sunt coeficienții asimptotici oblici.

În primul caz (cum x tinde spre plus infinit), se obține o asimptotă înclinată la dreapta, în al doilea (cum x tinde spre minus infinit), se obține o asimptotă oblică stângă. Asimptota oblică dreaptă este prezentată în Fig. de mai jos.

Când găsiți ecuația pentru o asimptotă oblică, este necesar să luați în considerare tendința lui X la plus infinit și minus infinit. Pentru unele funcții, de exemplu, cele raționale fracționale, aceste limite coincid, dar pentru multe funcții aceste limite sunt diferite și doar una dintre ele poate exista.

Dacă limitele coincid și x tinde spre plus infinit și minus infinit, linia dreaptă y = kx + b este asimptota cu două fețe a curbei.

Dacă cel puţin una dintre limitele care definesc asimptota y = kx + b , nu există, atunci graficul funcției nu are o asimptotă oblică (dar poate avea una verticală).

Este ușor de observat că asimptota orizontală y = b este un caz special de oblic y = kx + b la k = 0 .

Prin urmare, dacă în orice direcție o curbă are o asimptotă orizontală, atunci în această direcție nu există una înclinată și invers.

Exemplul 6. Găsiți asimptotele graficului unei funcții

Soluţie. Funcția este definită pe întreaga linie numerică, cu excepția x= 0, adică

Prin urmare, la punctul de rupere x= 0 curba poate avea o asimptotă verticală. Într-adevăr, limita funcției pe măsură ce x tinde spre zero din stânga este egală cu plus infinitul:

Prin urmare, x= 0 – asimptotă verticală a graficului acestei funcții.

Graficul acestei funcții nu are o asimptotă orizontală, deoarece limita funcției pe măsură ce x tinde spre plus infinit este egală cu plus infinit:

Să aflăm prezența unei asimptote oblice:

Am limite finite k= 2 și b= 0 . Drept y = 2x este asimptota înclinată în două sensuri a graficului acestei funcții (figura din interiorul exemplului).

Exemplul 7. Găsiți asimptotele graficului unei funcții

Soluţie. Funcția are un punct de întrerupere x= −1 . Să calculăm limitele unilaterale și să determinăm tipul de discontinuitate:

Concluzie: x= −1 este un punct de discontinuitate de al doilea fel, deci linia dreaptă x= −1 este asimptota verticală a graficului acestei funcții.

Căutăm asimptote oblice. Deoarece această funcție este fracționară-rațională, limitele la și la voi coincid. Astfel, găsim coeficienții pentru înlocuirea dreptei - asimptotă oblică în ecuație:

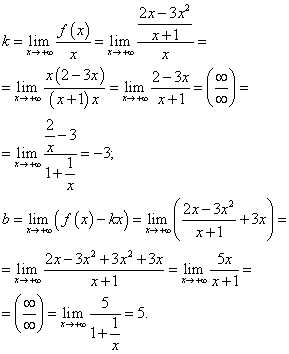
Înlocuind coeficienții găsiți în ecuația dreptei cu coeficientul de pantă, obținem ecuația asimptotei oblice:

y = −3x + 5 .

În figură este indicat graficul funcției culoare visiniu, iar asimptotele sunt afișate cu negru.

Exemplul 8. Găsiți asimptotele graficului unei funcții

Soluţie. Deoarece această funcție este continuă, graficul ei nu are asimptote verticale. Căutăm asimptote oblice:

Astfel, graficul acestei funcții are o asimptotă y= 0 at și nu are asyptot la .

Exemplul 9. Găsiți asimptotele graficului unei funcții

Soluţie. Mai întâi căutăm asimptotele verticale. Pentru a face acest lucru, găsim domeniul de definire al funcției. O funcție este definită atunci când inegalitatea și . Semnul variabilei x se potrivește cu semnul. Prin urmare, luați în considerare inegalitatea echivalentă. Din aceasta obtinem domeniul de definitie al functiei: . O asimptotă verticală poate fi doar la limita domeniului de definire a funcției. Dar x= 0 nu poate fi o asimptotă verticală, deoarece funcția este definită la x = 0 .

Luați în considerare limita din partea dreaptă la (nu există limită din partea stângă):

Punct x= 2 este un punct de discontinuitate de al doilea fel, deci linia dreaptă x= 2 - asimptota verticală a graficului acestei funcții.

Căutăm asimptote oblice:

Aşa, y = x+ 1 - asimptotă oblică a graficului acestei funcții la . Căutăm o asimptotă oblică la:

Aşa, y = −x − 1 - asimptotă oblică la .

Exemplul 10. Găsiți asimptotele graficului unei funcții

Soluţie. O funcție are un domeniu de definiție . Deoarece asimptota verticală a graficului acestei funcții poate fi doar la limita domeniului de definiție, găsim limitele unilaterale ale funcției la .

Asimptotele graficului unei funcții

Fantoma asimptotei rătăcește pe site de mult timp pentru a se concretiza în sfârșit într-un articol separat și a aduce o încântare deosebită cititorilor nedumeriți studiul complet al funcției. Găsirea asimptotelor unui grafic este una dintre puținele părți ale acestei sarcini care este acoperită în cursul școlar doar într-o manieră de ansamblu, deoarece evenimentele gravitează în jurul calculului. limitele funcției, dar încă se referă la matematică superioară. Pentru vizitatorii care înțeleg puțin analiza matematică, cred că indiciu este clar ;-) ...oprește-te, oprește-te, unde mergi? Limite- e usor!

Exemple de asimptote au fost întâlnite imediat în prima lecție despre grafice ale funcţiilor elementare, iar subiectul primește acum o analiză detaliată.

Deci, ce este o asimptotă?

Imagina punct variabil, care „călătorește” de-a lungul graficului funcției. Asimptota este Drept, la care aproape la nesfârşit graficul unei funcții se apropie pe măsură ce punctul ei variabil se deplasează la infinit.

Nota : Definiția este semnificativă, dacă aveți nevoie de o formulare în notație de calcul, vă rugăm să consultați manualul.

În plan, asimptotele sunt clasificate în funcție de locația lor naturală:

1) Asimptote verticale, care sunt date printr-o ecuație de forma , unde „alfa” este un număr real. Un reprezentant popular definește însăși axa ordonatelor,
cu o ușoară senzație de greață ne amintim de hiperbola.

2) Asimptote oblice scris în mod tradițional ecuația unei linii drepte cu un coeficient de unghi. Uneori grup separat evidențiați un caz special - asimptote orizontale. De exemplu, aceeași hiperbolă cu asimptotă.

Să mergem repede, să atingem subiectul cu o scurtă explozie de mitralieră:

Câte asimptote poate avea graficul unei funcții?

Nici unul, unul, doi, trei,... sau la infinit. Nu vom merge departe pentru exemple, să ne amintim functii elementare. O parabolă, o parabolă cubică și o undă sinusoidală nu au deloc asimptote. grafic exponential, funcţie logaritmică are o asimptotă unică. Arctangente și arccotangente au două dintre ele, iar tangenta și cotangente au infinit de multe. Nu este neobișnuit ca un grafic să aibă atât asimptote orizontale, cât și verticale. Hyperbole, te va iubi mereu.

Ce înseamnă?

Asimptotele verticale ale graficului unei funcții

Asimptota verticală a graficului este de obicei localizată în punctul de discontinuitate infinită funcții. Este simplu: dacă într-un punct funcția suferă o discontinuitate infinită, atunci linia dreaptă specificată de ecuație este asimptota verticală a graficului.

Nota : Rețineți că intrarea este folosită pentru a se referi la două concepte complet diferite. Dacă un punct este implicit sau o ecuație a unei drepte depinde de context.

Astfel, pentru a stabili prezența unei asimptote verticale într-un punct, este suficient să arătăm că cel putin unul din limitele unilaterale infinit. Cel mai adesea acesta este punctul în care numitorul funcției este zero. În esență, am găsit deja asimptote verticale în ultimele exemple ale lecției asupra continuităţii unei funcţii. Dar, în unele cazuri, există o singură limită unilaterală, iar dacă este infinită, atunci din nou - iubiți și favorizați asimptota verticală. Cea mai simplă ilustrație: și axa ordonatelor (vezi. Grafice și proprietăți ale funcțiilor elementare).

Din cele de mai sus, rezultă și un fapt evident: dacă funcția este pornită continuă, atunci nu există asimptote verticale. Din anumite motive, mi-a venit în minte o parabolă. Într-adevăr, unde poți „lipi” o linie dreaptă aici? ...da... înțeleg... adepții unchiului Freud erau isterici =)

Afirmația inversă este în general falsă: de exemplu, funcția nu este definită pe întreaga linie numerică, ci este complet lipsită de asimptote.

Asimptote înclinate ale graficului unei funcții

Asimptotele oblice (ca caz special - orizontale) pot fi trase dacă argumentul funcției tinde spre „plus infinit” sau „minus infinit”. De aceea graficul unei funcții nu poate avea mai mult de două asimptote oblice. De exemplu, graficul unei funcții exponențiale are o singură asimptotă orizontală la , iar graficul arctangentei la are două astfel de asimptote și altele diferite.

Când graficul din ambele locuri se apropie de o singură asimptotă oblică, atunci „infiniturile” sunt de obicei combinate sub o singură intrare. De exemplu, ...ai ghicit corect: .

Regula generală de bază:

Dacă sunt două final limită , atunci linia dreaptă este asimptota oblică a graficului funcției la . Dacă cel putin unul dintre limitele enumerate este infinită, atunci nu există nicio asimptotă oblică.

Nota : formulele rămân valabile dacă „x” tinde doar spre „plus infinit” sau doar către „minus infinit”.

Să arătăm că parabola nu are asimptote oblice:

Limita este infinită, ceea ce înseamnă că nu există nicio asimptotă oblică. Rețineți că în găsirea limitei nevoia a dispărut deoarece răspunsul a fost deja primit.

Nota : Dacă aveți (sau veți avea) dificultăți în înțelegerea semnelor plus-minus, minus-plus, vă rugăm să vedeți ajutorul de la începutul lecției
asupra funcţiilor infinitezimale, unde ți-am spus cum să interpretezi corect aceste semne.

Este evident că orice funcție pătratică, cubică, polinom de gradul 4 și superior nu are nici asimptote oblice.

Acum să ne asigurăm că și graficul nu are o asimptotă oblică. Pentru a dezvălui incertitudinea folosim Regula lui L'Hopital:
, care era ceea ce trebuia verificat.

Când funcția crește la infinit, totuși, nu există nicio linie dreaptă la care graficul ei s-ar apropia infinit de aproape.

Să trecem la partea practică a lecției:

Cum să găsiți asimptotele graficului unei funcții?

Exact așa este formulată sarcina tipică și implică găsirea TOATE asimptotele graficului (vertical, înclinat/orizontal). Deși, pentru a fi mai precis în a pune întrebarea, vorbim despre cercetarea prezenței asimptotelor (la urma urmei, s-ar putea să nu existe deloc). Să începem cu ceva simplu:

Exemplul 1

Găsiți asimptotele graficului unei funcții

Soluţie Este convenabil să o împărțim în două puncte:

1) Mai întâi verificăm dacă există asimptote verticale. Numitorul ajunge la zero la , și este imediat clar că în acest moment funcția are de suferit gol nesfârșit, iar linia dreaptă dată de ecuație este asimptota verticală a graficului funcției. Dar, înainte de a trage o astfel de concluzie, este necesar să se găsească limite unilaterale:

Vă reamintesc de tehnica de calcul pe care m-am concentrat în mod similar în articol Continuitatea funcției. Puncte de pauză. În expresia de sub semnul limită înlocuim . Nu există nimic interesant în numărător:
.

Dar la numitor se dovedește număr negativ infinitezimal:
, determină soarta limitei.

Limita din stânga este infinită și, în principiu, este deja posibil să se pronunțe despre prezența unei asimptote verticale. Dar limitele unilaterale sunt necesare nu numai pentru aceasta, ci AJUTĂ LA ÎNȚELEGE CUM localizați graficul funcției și construiți-l CORECT. Prin urmare, trebuie să calculăm și limita pentru dreapta:

Concluzie: limitele unilaterale sunt infinite, ceea ce înseamnă că linia dreaptă este asimptota verticală a graficului funcției la .

Prima limită finit, ceea ce înseamnă că este necesar să „continuați conversația” și să găsiți a doua limită:

Și a doua limită finit.

Astfel, asimptota noastră este:

Concluzie: dreapta dată de ecuație este asimptota orizontală a graficului funcției la .

Pentru a găsi asimptota orizontală
puteți folosi o formulă simplificată:

Daca exista finit limită, atunci linia dreaptă este asimptota orizontală a graficului funcției la .

Este ușor de observat că numărătorul și numitorul funcției aceeași ordine de creștere, ceea ce înseamnă că limita căutată va fi finită:

Răspuns:

În funcție de condiție, nu trebuie să finalizați desenul, dar dacă este în plină desfășurare studiul funcției, apoi pe schiță facem imediat o schiță:

Pe baza celor trei limite găsite, încercați să vă dați seama singur cum ar putea fi localizat graficul funcției. Este deloc greu? Găsiți 5-6-7-8 puncte și marcați-le pe desen. Cu toate acestea, graficul acestei funcții este construit folosind transformări ale graficului unei funcţii elementare, iar cititorii care au examinat cu atenție Exemplul 21 al articolului de mai sus pot ghici cu ușurință ce fel de curbă este aceasta.

Exemplul 2

Găsiți asimptotele graficului unei funcții

În practică, funcțiile fracționale-raționale sunt cel mai des întâlnite, iar după antrenamentul pe hiperbole, vom complica sarcina:

Exemplul 3

Găsiți asimptotele graficului unei funcții

Soluţie: Unu, doi și gata:

1) Sunt localizate asimptotele verticale în puncte de discontinuitate infinită, deci trebuie să verificați dacă numitorul ajunge la zero. Să decidem ecuație pătratică:

Discriminantul este pozitiv, deci ecuația are două rădăcini reale, iar munca este crescută semnificativ =)

Pentru a găsi în continuare limite unilaterale, este convenabil să factorizezi trinomul pătrat:
(pentru notarea compactă, „minus” a fost inclus în prima paranteză). Pentru a fi în siguranță, haideți să verificăm prin deschiderea parantezelor mental sau la curent.

Să rescriem funcția în formă

Să găsim limite unilaterale la punctul:

Și la punctul:

Astfel, liniile drepte sunt asimptote verticale ale graficului funcției în cauză.

2) Dacă te uiți la funcție , atunci este destul de evident că limita va fi finită și avem o asimptotă orizontală. Să-i arătăm prezența pe scurt:

Astfel, linia dreaptă (axa absciselor) este asimptota orizontală a graficului acestei funcții.

Răspuns:

Limitele și asimptotele găsite oferă o mulțime de informații despre graficul funcției. Încercați să vă imaginați mental desenul ținând cont de următoarele fapte:

Schițați versiunea dvs. a graficului pe schița dvs.

Desigur, limitele găsite nu determină clar aspectul graficului și este posibil să faceți o greșeală, dar exercițiul în sine vă va oferi un ajutor neprețuit în timpul studiu complet al funcției. Poza corectă este la sfârșitul lecției.

Exemplul 4

Găsiți asimptotele graficului unei funcții

Exemplul 5

Găsiți asimptotele graficului unei funcții

Acestea sunt sarcini pentru soluții independente. Ambele grafice au din nou asimptote orizontale, care sunt imediat detectate de următoarele caracteristici: în Exemplul 4 ordinea de crestere numitor Mai mult, decât ordinea de creștere a numărătorului, iar în Exemplul 5 numărătorul și numitorul aceeași ordine de creștere. În soluția de probă, prima funcție este examinată pentru prezența asimptotelor oblice în totalitate, iar a doua - prin limită.

Asimptotele orizontale, în impresia mea subiectivă, sunt vizibil mai frecvente decât cele care sunt „cu adevărat înclinate”. Cazul general mult așteptat:

Exemplul 6

Găsiți asimptotele graficului unei funcții

Soluţie: clasic al genului:

1) Deoarece numitorul este pozitiv, atunci funcția continuu de-a lungul întregii linii numerice și nu există asimptote verticale. ...Este bun? Nu este cuvântul potrivit - excelent! Punctul nr. 1 este închis.

2) Să verificăm prezența asimptotelor oblice:

Prima limită finit, deci să mergem mai departe. În timpul calculului a doua limită de eliminat incertitudine „infinit minus infinit” Aducem expresia la un numitor comun: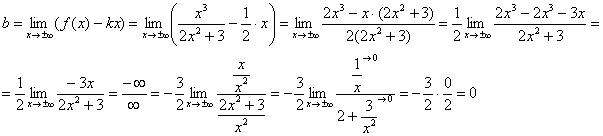

Și a doua limită finit Prin urmare, graficul funcției în cauză are o asimptotă oblică:

Concluzie:

Astfel, când graficul funcției infinit de aproape se apropie de o linie dreaptă:

Exemplul 7

Găsiți asimptotele graficului unei funcții

Soluţie: Nu este nimic special de comentat, așa că voi elabora un exemplu aproximativ de soluție curată:

1) Asimptote verticale. Să explorăm ideea.

Linia dreaptă este asimptota verticală pentru graficul de la .

2) Asimptote oblice:

Linia dreaptă este asimptota înclinată pentru graficul de la .

Răspuns:

Limitele și asimptotele unilaterale găsite ne permit să prezicem cu mare încredere cum arată graficul acestei funcții. Desenul corect la sfârșitul lecției.

Exemplul 8

Găsiți asimptotele graficului unei funcții

Evident, deținătorii de asimptote oblice „reale” sunt graficele acelor funcții raționale fracționale al căror cel mai înalt grad de numărător încă unul cel mai înalt grad al numitorului. Dacă este mai mult, nu va exista nicio asimptotă oblică (de exemplu, ).

Dar alte miracole se întâmplă în viață:

Exemplul 9

Exemplul 11

Examinați graficul unei funcții pentru prezența asimptotelor

Soluţie: este evident că , deci considerăm doar semiplanul drept, unde există un grafic al funcției.

Astfel, linia dreaptă (axa ordonatelor) este asimptota verticală pentru graficul funcției la .

2) Studiul asupra asimptotei oblice poate fi efectuat conform schemei complete, dar în articol Regulile lui L'Hopital am aflat că funcţie liniară Mai mult ordin înalt creștere decât logaritmică, prin urmare: (Vezi Exemplul 1 al aceleiași lecții).